https://www.acmicpc.net/problem/1958
1958번: LCS 3
첫 줄에는 첫 번째 문자열이, 둘째 줄에는 두 번째 문자열이, 셋째 줄에는 세 번째 문자열이 주어진다. 각 문자열은 알파벳 소문자로 이루어져 있고, 길이는 100보다 작거나 같다.
www.acmicpc.net

문제 분석
LCS란 최장 공통 부분수열이다.
만약 문자열이 두 개(예제 입력 1의 위 두 문자열)라고 가정하였을 때, 다이나믹 프로그래밍(DP)를 사용하여 쉽게 LCS를 계산할 수 있다.
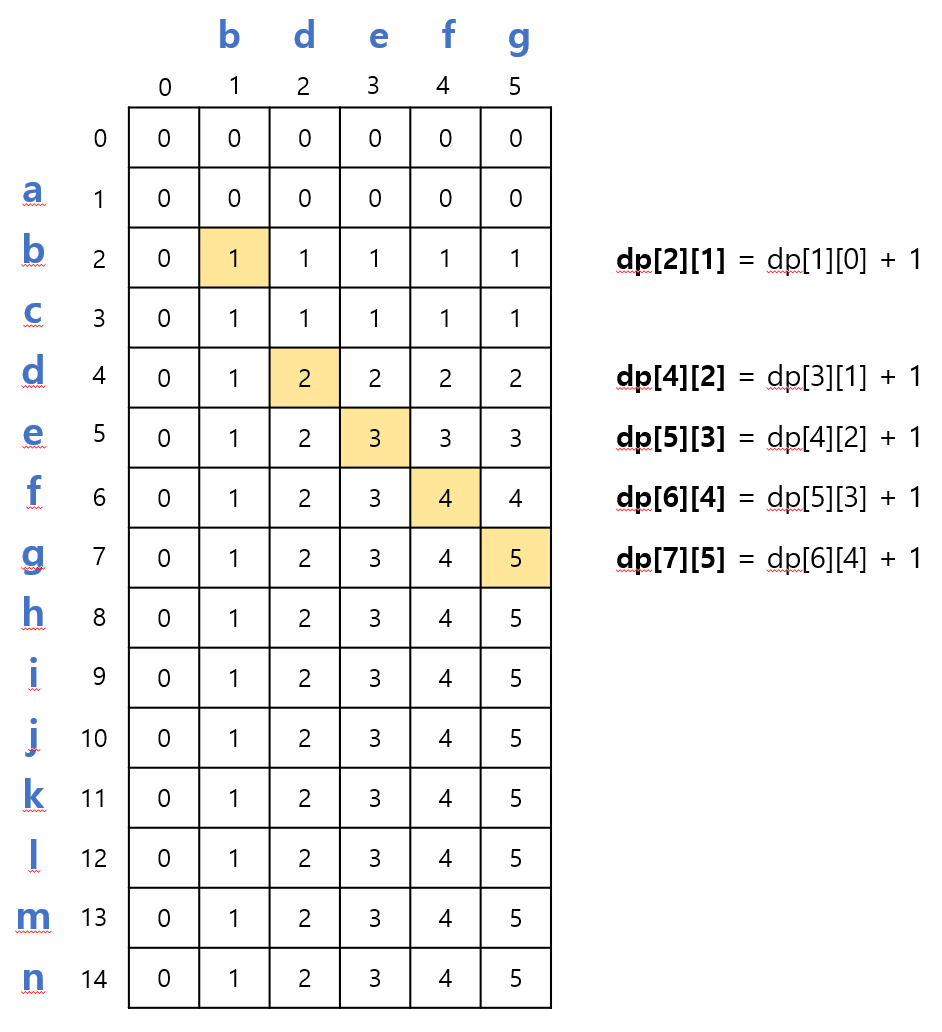
위의 그림과 같이
두 문자열을 앞에 공백이 있는 이차원 리스트로 만든다.
그 후 이중 반복문을 돌면서 같은 문자열이 있는지 탐색한다.
1. 같은 문자를 만난 경우
이 때, 같은 문자를 만난다면 대각선 왼쪽 위에 있는 수에 1을 더한 값을 가진다.
그 이유는 [4][2]을 예로 들면
왼쪽 문자열에서 abc, 위쪽 문자열에서 b가 되며 두 문자열이 같은 문자열을 만나기 전의 문자열을 가져야 하기 때문이다.
그리고 그 값에 같은 문자열이 추가되기 때문에 1을 더하여 리스트의 값을 바꿔준다.
2. 다른 문자를 만난 경우
만약 문자가 같지 않다면 바로 왼쪽 값과 위쪽 값을 비교하여 큰 값을 가진다.
[2][3]을 예로 들면, (ab, bde)는 (ab, bd), (a, bde)를 비교하게 된다.
그 이유는 위쪽 문자열에서 e를 추가할 때 (ab, bd)를 비교하여 최대 길이인 1을 유지할 수 있고
왼쪽 문자열에서 b를 추가할 때 (a, bde)를 비교하여 최대 길이인 0을 유지하게 된다.
따라서 [2][3]에서는 e와 b가 동시에 추가되기 때문에 두 가지의 경우 중 최대 길이를 갖게 되는 것이다.
for i in range(len(one)):
for j in range(len(two)):
if i == 0 or j == 0:
dp[i][j] = 0
elif one[i] == two[j]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])대각선의 값을 계산하기 때문에 맨 앞의 공백을 추가하였다.
그러므로 계산 과정에서 i가 0이거나 j가 0일 때 값을 0으로 넣어주어야 한다.
위의 예시는 문자열을 두 개로 LCS를 구하는 방법이었다.
하지만 문제는 세 개의 문자열을 가지고 LCS를 구해야 한다.
차원을 확장시켜보면 쉽게 계산이 가능하다.
기존에 2차원 리스트였던 것을 3차원 리스트로 확장하고 x축, y축, z축이라고 가정했을 때
모든 축의 값이 동일해야 같은 문자를 만난 경우라고 생각하면 된다.
그 후 값의 비교는 축을 하나 추가하였기 때문에 3개의 값을 비교하여 계산한다.
for i in range(len(one)):
for j in range(len(two)):
for k in range(len(three)):
if i == 0 or j == 0 or k == 0:
dp[i][j][k] = 0
elif one[i] == two[j] and two[j] == three[k]:
dp[i][j][k] = dp[i - 1][j - 1][k - 1] + 1
else:
dp[i][j][k] = max(dp[i - 1][j][k], dp[i][j - 1][k], dp[i][j][k - 1])
위의 로직을 통해 3차원 리스트를 가지고 LCS를 구하면 된다.
코드
words = []
for _ in range(3):
words.append(" " + input())
def lcs(one, two, three):
dp = [
[[0 for _ in range(len(three))] for _ in range(len(two))]
for _ in range(len(one))
]
for i in range(len(one)):
for j in range(len(two)):
for k in range(len(three)):
if i == 0 or j == 0 or k == 0:
dp[i][j][k] = 0
elif one[i] == two[j] and two[j] == three[k]:
dp[i][j][k] = dp[i - 1][j - 1][k - 1] + 1
else:
dp[i][j][k] = max(dp[i - 1][j][k], dp[i][j - 1][k], dp[i][j][k - 1])
return dp[len(one) - 1][len(two) - 1][len(three) - 1]
print(lcs(words[0], words[1], words[2]))'알고리즘 > 백준' 카테고리의 다른 글
| [백준/Python] 17404번: RGB거리 2 (0) | 2023.02.08 |
|---|---|
| [백준/Python] 10942번: 팰린드롬? (0) | 2023.02.01 |
| [백준/Python] 2961번: 도영이가 만든 맛있는 음식 (0) | 2023.01.30 |
| [백준/Python] 1205번: 등수 구하기 (0) | 2023.01.27 |
| [백준/Python] 2448번: 별 찍기 - 11 (0) | 2023.01.26 |